Involute gears

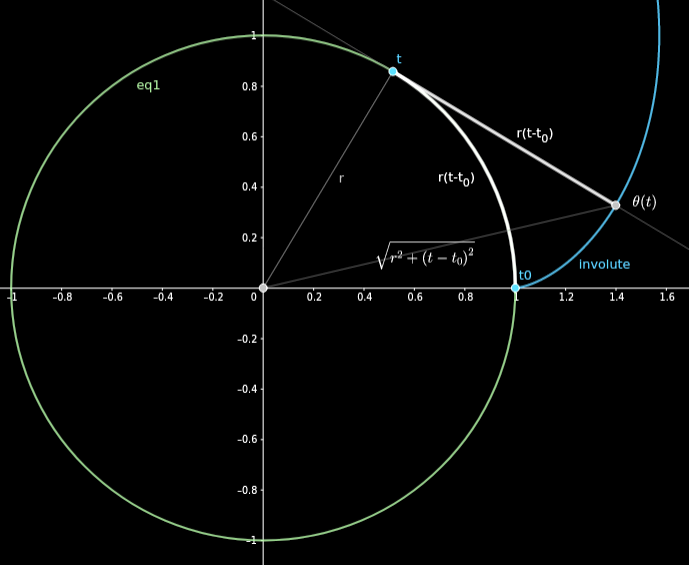
Involute curve

Those are very impor\tant for involute gears, check at wikipedia for more details

• Involute for any \( \vec \gamma \) curve (with parameter \(t\)):

\[\vec \theta(t) = \vec \gamma(t) + \vec \gamma'(t) \times (t_0 - t)\]

• Parametric equation of a circle (with radius r):

\[\begin{split}\vec \gamma(t) = r \begin{pmatrix} \cos(t) \\ \sin(t) \end{pmatrix}\end{split}\]

Thus, we obtain the involute of circle (with radius \(r\)):

\[\begin{split}\vec \theta(t) = r \begin{pmatrix} \cos(t) \\ \sin(t) \end{pmatrix} + r (t_0-t) \begin{pmatrix} -\sin(t) \\ \cos(t) \end{pmatrix} \end{split}\]

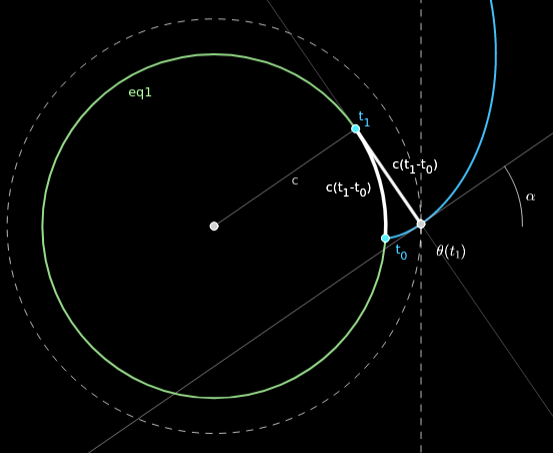
Few remarks

An involute is symetric over \(t_0\):

• \( \vec \theta([t_0, +\infty[) \) is an involute developed by a direct rotation
• \( \vec \theta(]-\infty, t_0]) \) is an involute developed by a reverse rotation

A gear tooth

Parameters

• \( s = \) gear step (distance on the primitive)
• \( z = \) number of tooths on the gear
• \( \alpha = \) pressure angle (angle of the rack tooth)
• \( h = \) rack half height = \( (\text{total height}) / 2 \)
• \( e = \) (offset) amount to shift up the top and bottom of the rack, it does not change the tooth sides.
• \( x = \) fraction of the rack above the primitive (close to 0.5), usually \( = 0.5 + 2 \times e / p \times \\tan(\alpha) \)

Useful circles

• \( p = \) primitive radius \( = (s \times z) / (2 \pi) \)
• \( c = \) base circle radius \( = p \times \cos(\alpha) \)
• \( p - h + e = \) bottom circle radius
• \( p + h + e = \) top circle radius

Curves

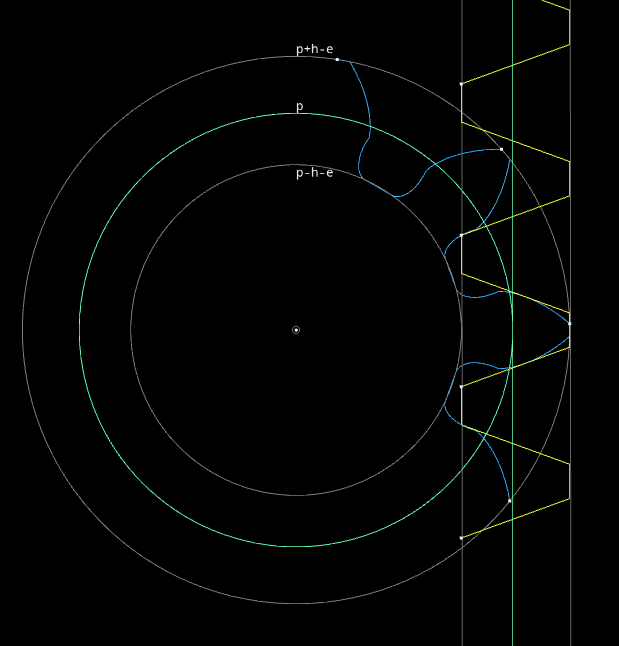
The contact that transmits the torque is always oriented toward the rack tooth normal (angle \(\alpha\)). The only solution for this is to have the contact point moving on an axis from the contact between both primitives, and oriented along \(\alpha\)

The contact curve is then an involute of circle.

\[\begin{split}\vec \theta_0(t) = \text{contact curve} = c \begin{pmatrix} \cos(t) \\ \sin(t) \end{pmatrix} + c (t_0-t) \begin{pmatrix} -\sin(t) \\ \cos(t) \end{pmatrix} \end{split}\]

As the tooth is moving in/out of the gear, its opposite corner to the contact point may collide with a next tooth. This interference force us to remove material from the tooth, u\sing the interference curve.

The interference curve is then an involute of circle with a radial offset.

\[\begin{split}\vec \theta_i(t) = \text{interference curve} = p \begin{pmatrix} \cos(t) \\ \sin(t) \end{pmatrix} + p (t_i-t) \begin{pmatrix} -\sin(t) \\ \cos(t) \end{pmatrix} - (h+e) \begin{pmatrix} \cos(t) \\ \sin(t) \end{pmatrix}\end{split}\]

Start points

If we consider a period starting from the middle of the tooth top, there is two places our curves start (one each tooth). We can define them relatively to the cros\sing point between the primitive circle and the involute.

Cros\sing point between primitive circle and involute: \( t_s = \{ m / p \times x / 2, m / p \times (2 - x) / 2 \} \)

Value of \( t_0 \)

It can be determined relatively to \( t_s \) which is the place (but not the parameter) where \( \vec \theta_0 \) reaches radius \( p \) :

\[\begin{split}\begin{align} & \Vert \vec \theta_0(t) \Vert = p \\ \iff & p^2 = \Vert \vec \theta_0(t) \Vert^2 = c^2 \times ( 1 + (t-t_0)^2 ) \\ \iff & t - t_0 = \sqrt{\left(\frac p c \right)^2 - 1} = \tan(\alpha) \end{align}\end{split}\]

We just need to take the angle for the obtained \( t \)

\[t_0 - t_s = \angle{\left( \vec \theta(t_0 + \tan(\alpha)) - \theta(t_0) \right)} \]

Value of \( t_i \)

\( \vec \theta_i \) starts at the very moment the tooth offset is radial:

\[t_i - t_s = \frac{\text{arctan}(h-e)}{p \times tan(\alpha) }\]

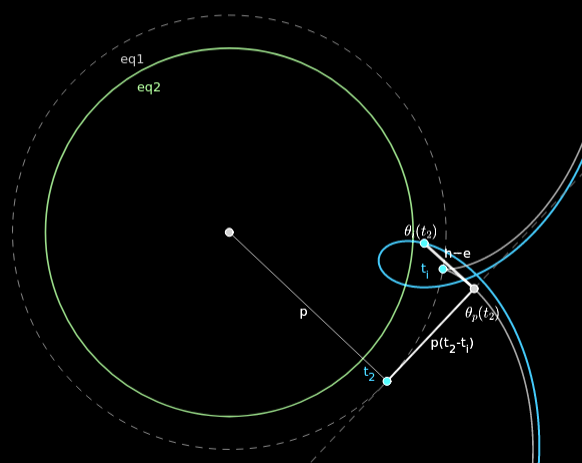
Intersection between \( \vec \theta_0 \) and \( \theta_i \)

To know when does \( \vec \theta_i \) stop and when \( \theta_0 \) start, we need to know the intersection point between them. As both curves are defined by different points of the rack at different times during the rotation, the two curves must have different parameters.

Intersection between \(\vec \theta_0\) and \(\theta_i\)

\[\begin{split}\begin{align} & \vec \theta_0(t_1) = \theta_i(t_2) \\ \iff & \vec \theta_0(t_1) - \theta_i(t_2) = \vec 0 \\ \end{align}\end{split}\]

The equation becomes quite complicated, so we can use the Newton’s method to solve it

\[\begin{split}\begin{align} f(t_1, t_2) & = \vec \theta_0(t_1) - \theta_i(t_2) \\ & = c \begin{pmatrix} \cos(t_1) \\ \sin(t_1) \end{pmatrix} + c (t_0-t_1) \begin{pmatrix} -\sin(t_1) \\ \cos(t_1) \end{pmatrix} \\ & - p \begin{pmatrix} \cos(t_2) \\ \sin(t_2) \end{pmatrix} + p (t_i-t_2) \begin{pmatrix} -\sin(t_2) \\ \cos(t_2) \end{pmatrix} - (h-e) \begin{pmatrix} \cos(t_2) \\ \sin(t_2) \end{pmatrix} \end{align}\end{split}\]

• Its jacobian matrix:

\[\begin{split}J(f) = \begin{bmatrix} \frac{\delta f}{\delta t_1} \\ \frac{ \delta f }{ \delta t_2 } \end{bmatrix} = \begin{bmatrix} -c (t_0 - t_1) \begin{pmatrix} \cos(t_1) \\ \sin(t_1) \end{pmatrix} \\ p (t_i - t_2) \begin{pmatrix} \cos(t_2) \\ \sin(t_2) \end{pmatrix} + (h-e) \begin{pmatrix} -\sin(t2)) \\ \cos(t_2) \end{pmatrix} \end{bmatrix}\end{split}\]

• The Newton method consists in doing the following formula by iterations (until the necessary precision is reached)

\[\begin{split}\begin{pmatrix} t_1 \\ t_2 \end{pmatrix} \leftarrow \begin{pmatrix} t_1 \\ t_2 \end{pmatrix} - J^{-1}(f)(t_1, t_2) \times f(t_1, t_2)\end{split}\]

To make sure it will converge to the desired solution, we need to take an initial state in the convex zone of the solution:

• \(t_1\) on the primitive circle:

\[t_{1,\text(initial)} = t_0 - \tan(\alpha)\]

• \(t_2\) on the base circle:

\[t_{2,\text(initial)} = t_i + \frac{\sqrt{ c^2 - (p-h+e)^2 }} p \]

It ends with the parameters \( t_1, t_2 \) of \( \vec \theta_0, \theta_i \) at the intersection.

• \( \vec \theta_i \) must stop at the intersection at \( t_2 \)
• \( \vec \theta_0 \) must start at the intersection at \( t_1 \)

Stop point \(t_3\) of \( \vec \theta_0 \)

• In case \( \vec \theta_0 \) hits the top circle

\[t_3 - t_0 = \frac{\sqrt{ (p+h+e)^2 - c^2 }} c \]

• In case \( \vec \theta_0 \) hits the involute of the next period

We know that it will cross on the period-start axis \( (O, \vec x) \), so

\[\begin{split}\begin{align} & \vec \theta_0(t_3) \cdot \vec y = 0 \\ \iff & 0 = \sin(t_3) + \cos(t_3) (t_0-t_3) = f(t) \end{align}\end{split}\]

A simple Newton’s method solves this with initial state on the top circle