joints - Kinematic Joints definition
Simple joints
-
class
Ball(s1, s2, p1, p2=None)[source] Joint for rotation all around a point.
Classical definition: Ball (point) the initial state doen’t require more data the class holds a point for each side

-
class
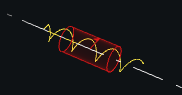
Pivot(s1, s2, a1, a2=None, position=None)[source] Junction for rotation only around an axis
Classical definition: Pivot (axis) no additional information is required by the initial state this class holds an axis for each side
-
class
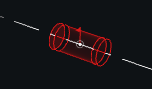
Gliding(s1, s2, a1, a2=None, position=None)[source] Joint for rotation and translation around an axis
Classical definition: Gliding pivot (axis) the initial state doesn’t require more data this class holds an axis for each side
-
class
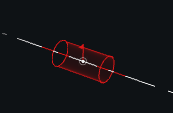
Track(s1, s2, b1, b2=None, position=None)[source] Joint for translation only in a direction
Classical definition: Track (direction vector) the initial state requires more parameters: the relative placements of the solids this class holds a base for each of the solids, bases are (0,X,Y) where X,Y are constrained to keep the same direction across bases, and the bases origins lays on their common Z axis
-
class
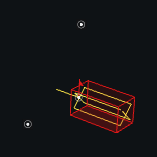
Punctiform(s1, s2, a1, p2=None)[source] Joint for rotation all around a point belonging to a plane.
Classical definition: Punctiform/Sphere-Plane (axis) The initial state does not require more data The class holds a normal axis for the plane side, and a point for the sphere side (that defaults to the axis’ origin)
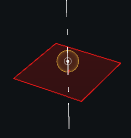
-
class
Planar(s1, s2, a1, a2=None, position=None)[source] Joint for translation in 2 directions and rotation around the third direction
Classical definition: Planar (direction vector) the initial state requires an additional distance between the solids this class holds an axis for each side, the axis origins are constrained to share the same projections on the normal
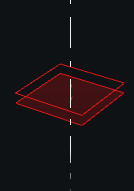
Complex joints
-
class
Gear(s1, s2, ratio, a1, a2=None, position=None)[source] Gear interaction between two solids.
ratiois the factor from the rotation of s1 to the rotation of s2 The two pinions are considered circular, but no assumption is made on their radius or relative inclination. The interaction is symetric.Note
As solids don’t hold more data than only their pose (position and orientation), there is no way to distinguish the gear in a pose, and in the same pose rotated by \(2 \pi\).
Therefore rotation jumps can occurs when several gears are tied.
-
class
Helicoid(s0, s1, step, b0, b1=None, position=None)[source] Screw a solid into an other.
stepis the translation distance needed for that one solid turn by 2*pi around the other The interaction is symetric.Note
As solids orientation is in \([0;~ 2 \pi]\), when the gap in the helicoid is bigger than
stepthen the joints solids only rotates bygap/step * 2*pi % 2*piIf the helicoid is involved in any gearings or reductors, the result might be not what was expected.