primitives - 3D Primitives for Wire generation

Primitives are parametrized objects, that can be baked into a mesh/web/wire object. A primitive object must have the following signature:

class SomePrimitive:
        # method baking the primitive in some general-purpose 3D object
        # resolution is optional and defaults to the primitive settings
        # that defaults to the current settings at call time
        def mesh(self, resolution=None) -> Mesh/Web/Wire:
                ...

        # for the solver
        # primitive attributes the solver has to consider as variables or variable container
        slvvars = 'fields', 'for', 'solver', 'variables'
        # optional method constraining the primitive parameters (to keep points on a circle for instance)
        def fit(self) -> err**2 as float:
                ...

isprimitive(obj)

Return True if obj match the signature for primitives

Curve resolution

Some primitive types are curves, the discretization is important for visual as well as for result quality (remember that even if something looks like a perfect curves, it’s still polygons). The resolution (subdivision) of curve is done following the following criterion present in the settings module

Specification priority order:

1. Optional argument resolution passed to primitive.mesh() or to web() or wire()
2. Optional attribute resolution of the primitive object
3. Value of settings.primitives['curve_resolution'] at bake time.

Specification format:

('fixed', 16)   # fixed amount of 16 subdivisions
('rad', 0.6)    # max polygon angle is 0.6 rad
('radm', 0.6)
('radm2', 0.6)

Primitives types

class Vector

Alias to vec3

class Point

Alias to vec3

class Axis(origin, direction, interval=None)

Mimic the behavior of a tuple, but with the primitive signature.

__getitem__(i)

behave like the axis was a tuple (origin, direction)

flip() → Axis

switch the axis direction

offset(increment) → Axis

move the axis origin along its direction

transform(transform) → Axis

move the axis by the given transformation

isaxis(obj)

Return True if the given object is considered to be an axis. An axis can be an instance of Axis or a tuple (vec3, vec3)

class Segment(a, b)

Segment from a to b

property direction

class ArcCentered(axis, a, b, resolution=None)

Arc from a to b, centered around the origin of the axis.

An axis is requested instead of a point (that would be more intuitive), to solve the problem when a,b, center are aligned

property center

property radius

tangent(pt)

Tangent to the closest point of the curve to pt

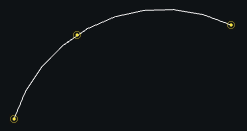
class ArcThrough(a, b, c, resolution=None)

Arc from a to c, passing through b

property center

property radius

property axis

tangent(pt)

Tangent to the closest point of the curve to pt

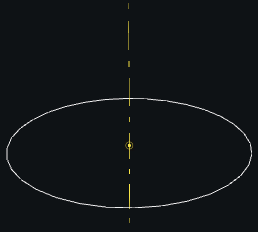
class Circle(axis, radius, alignment=dvec3(1, 0, 0), resolution=None)

Circle centered around the axis origin, with the given radius, in an orthogonal plane to the axis direction

property center

tangent(pt)

Tangent to the closest point of the curve to pt

class ArcTangent(a, b, c, resolution=None)

An arc always tangent to Segment(a,b) and Segment(c,b). The solution is unique.

property center

property radius

property axis

tangent(pt)

Tangent to the closest point of the curve to pt

class TangentEllipsis(a, b, c, resolution=None)

An quater of ellipsis always tangent to Segment(a,b) and Segment(c,b). The solution is unique.

property center

property axis

tangent(pt)

Tangent to the closest point of the curve to pt

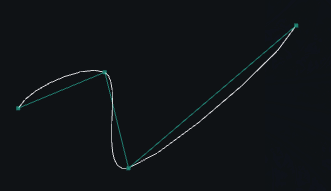
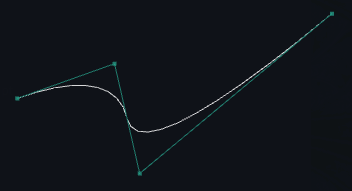
class Interpolated(points, weights=None, resolution=None)

Interpolated curve passing through the given points (3rd degree bezier spline)

The tangent in each point is determined by the direction between adjacent points The point weights is how flattened is the curve close to the point tangents

class Softened(points, weights=None, resolution=None)

Interpolated curve tangent to each segment midpoint (3rd degree bezier curve)

The points weights is the weight in the determination of each midpoint